
Everything was coined or bottom-bent, which meant that resulting in the punch tip's radius always was achieved. In the past, it wasn't as important to know precisely what the resulting inside radius was. Either way, the charts worked for each of them but may not have worked when applied to another shop's set of circumstances. Some charts actually measured the resulting inside radius and found the correct bend deduction. (0.81mm) bend radius by virtue of the punch tip's radii." Using this criteria, the creator approximated the punch radius rather than measured the In other words, each chart creator must have said something like, "This is the value of a 1/32-in. This leads to the question, Which chart is correct? The answer is, All of them! They all are correct for the environment in which they were created. For example, a part with three bends could have as much error as 0.117 in. Top and bottom values can make a good part a bad one quickly. However, if tight tolerancing or if multiple bends are involved, the difference between the Assuming that you have a generous tolerance over one bend, the error in bend deduction can be spread out, and a good part still can be produced.
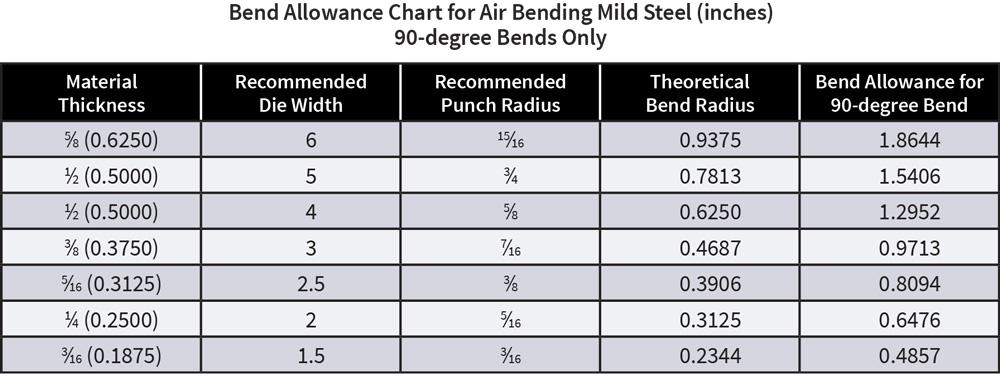
The total error, or amount of difference between the top and the bottom entries, was 0.039 in. Figure 1 shows data from five of those charts selected at random.

In reviewing a couple dozen bend deduction charts from a variety of sources, I couldn't find any that agreed with another, with the exception of a single number here and there.


 0 kommentar(er)
0 kommentar(er)
